Overview

Hello folks! Hope you are learning something productive.

In the previous blog, I discuss why we actually required to use Tree Data Structure when it comes to the huge data. Today, I will discuss one of the most important topic related to both interviews and competitive programming perspective, i.e. Traversing the Binary Search Tree.

Usually there are many ways to traverse the Tree Data Structure but in this blog post, I am discussing three most important traversing technique

1. Preorder Traversing

2. Inorder Traversing

3. Postorder Traversing

And the best part is, you don't need any technique or prior knowledge to understand this concepts other than your and everyone favorite one i.e. recursion.

Introduction

First we start our topic and understand the traversing technique, first we understand what is actually the word Traversing mean?

In the simple language, Traversing is way to iterate each and every element present in the data structure.

Let's move on and try to understand the different traversing algorithm for binary search tree.

1. Preorder Traversing

Preorder Traversing is a traversing technique in which we iterate the root element followed by the left element and the right element.

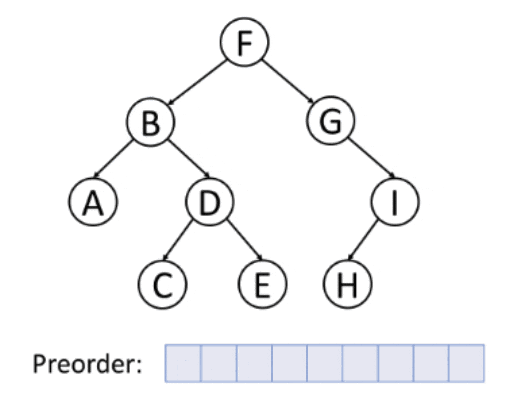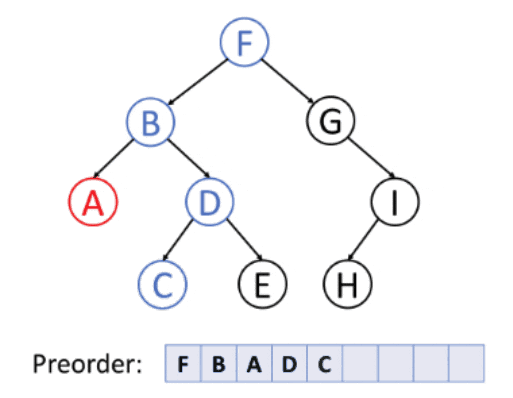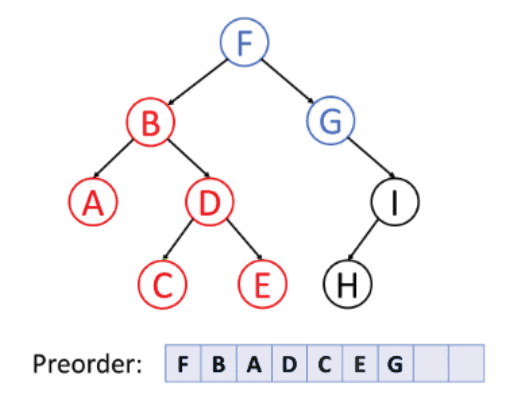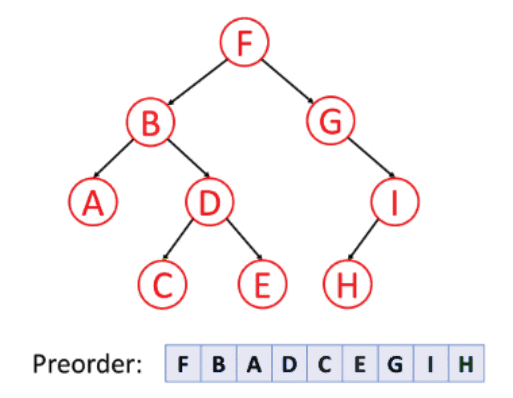
Algorithm

1. Traverse the root element.
2. Move the pointer to the left node of the root and traverse that node.
3. After completely traversing the left part of the root node, move the pointer to the right node of the root and traverse that node.

public void preOrder(Node root) {
    if(root == null) {    // base condition
        return;
    }
    System.out.println(root.data); // traverse root node
    postOrder(root.left);   // traverse left node
    postOrder(root.right);  // traverse right node
}

2. Inorder Traversing

Inorder Traversing is a traversing technique in which we iterate the left node element followed by the root element and the right element.

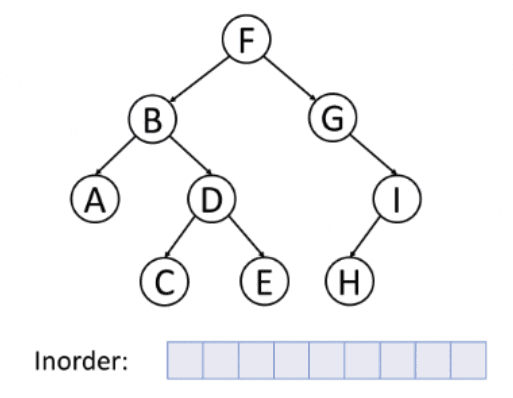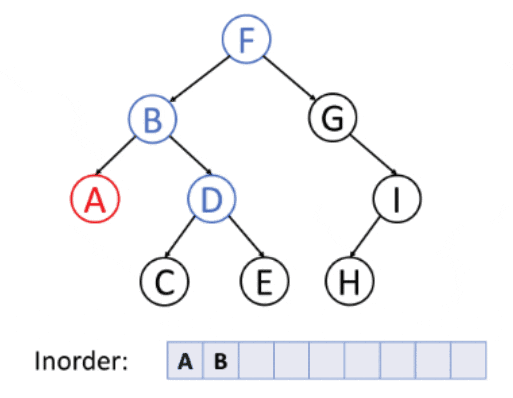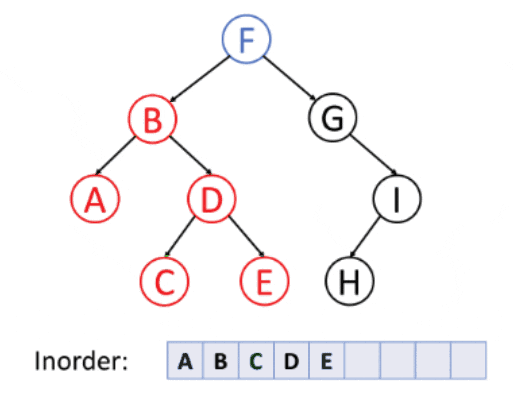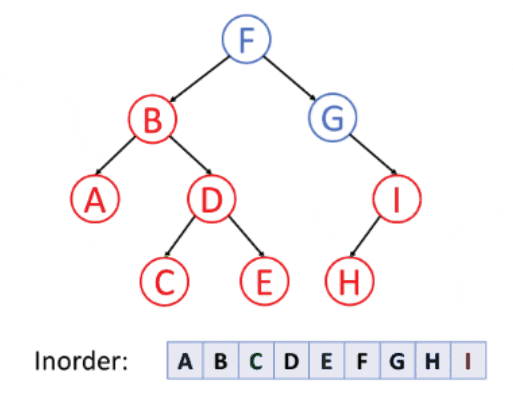
Algorithm

1. Traverse the left node element.
2. Move the pointer to the root node of the left node and traverse that node.
3. After completely traversing the left and the root node, move the pointer to the right node of the root and traverse that node.

public void inOrder(Node root) {
    if(root == null) {    // base condition
        return;
    }
    inOrder(root.left);   // traverse left node
    System.out.println(root.data); // traverse root node
    inOrder(root.right);  // traverse right node
}

💡In binary search tree, Inorder traversing returns the sorted tree data structure.

3. Postorder Traversing

Postorder Traversing is a traversing technique in which we iterate the right node element followed by the left element and the root element.

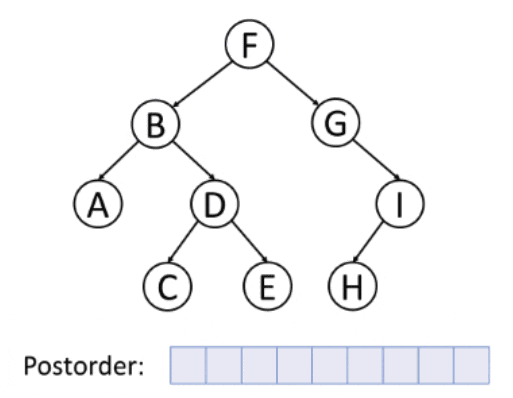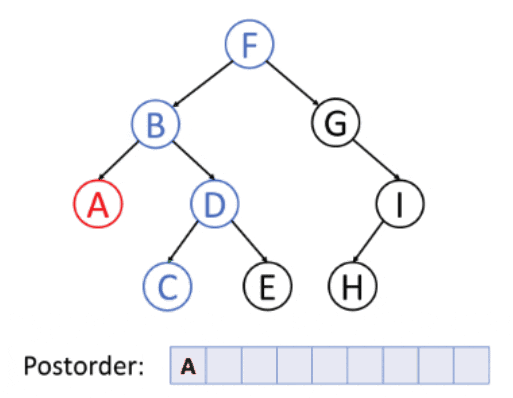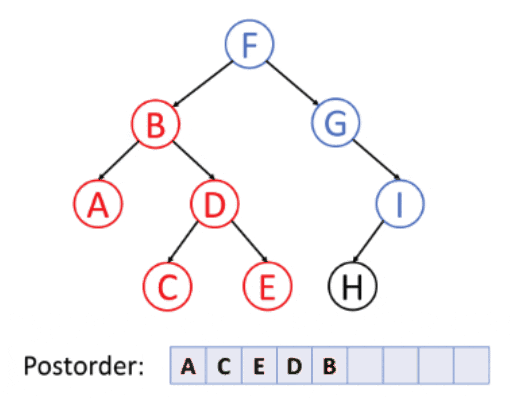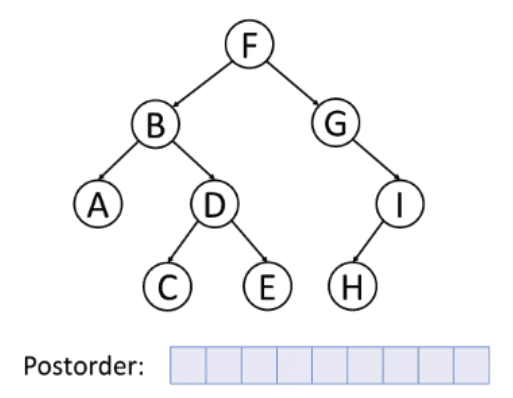
Algorithm

1. Traverse the right node element.
2. Move the pointer to the left node of the root node and traverse that node.
3. After completely traversing the right and the left node, move the pointer to the root node and traverse that node.

public void postOrder(Node root) {
    if(root == null) {    // base condition
        return;
    }
    inOrder(root.left);   // traverse left node
    inOrder(root.right);  // traverse right node
    System.out.println(root.data); // traverse root node
}

Conclusion

All three traversing technique are quiet similar with each other which makes these algorithm super easy to understand and implement. But the real challenge arise when move to the coding platform and try to solve those problem. If we had a great understanding of these concepts, it will become easier to solve those problem.

Subscribe to the newsletter to read more blogs on data structures and algorithms!