Overview

Most of the time while doing competitive programming over different platforms, we get an Time Limit Exceed (TLE). For Example: While solving the unique BST problem on Leetcode, we had different approaches to solve that question, sometimes we succeed while sometimes we just move on to the different question.

In this blog post, we are discussing what catalan number is and what are the different application where we can apply catalan number. Also we are solving the unique BST problem.

So, what are you waiting for? Let's gets started.

What is Catalan Number?

According to Wikipedia, The Catalan numbers are a sequence of natural numbers that occur in various counting problems, often involving recursively defined objects. It is denoted by (C_n).

🗒️It can be used only when we non-negative integers.

With catalan number, we get a sequence like:

C₀ = 1

C₁ = 1

C₂ = C₀ C₁ + C₁ C₀ = 2

C₃ = C₀ C₂ + C₁ C₁ + C₂ C₀ = 5

With this sequence, we get a formula: C_n = C[i] x C[n - i - 1]

For more understanding related to the topic you can check out the link mathworld.wolfram.com/CatalanNumber.html

Application of Catalan Number

1. Unique BST
2. Parenthesis/bracket combination
3. Possible forest
4. Ways of triangulation
5. Possible paths in matrix
6. Dividing a circle using N chords
7. Dyck words of given length.

Use Catalan Number to solve Unique BST

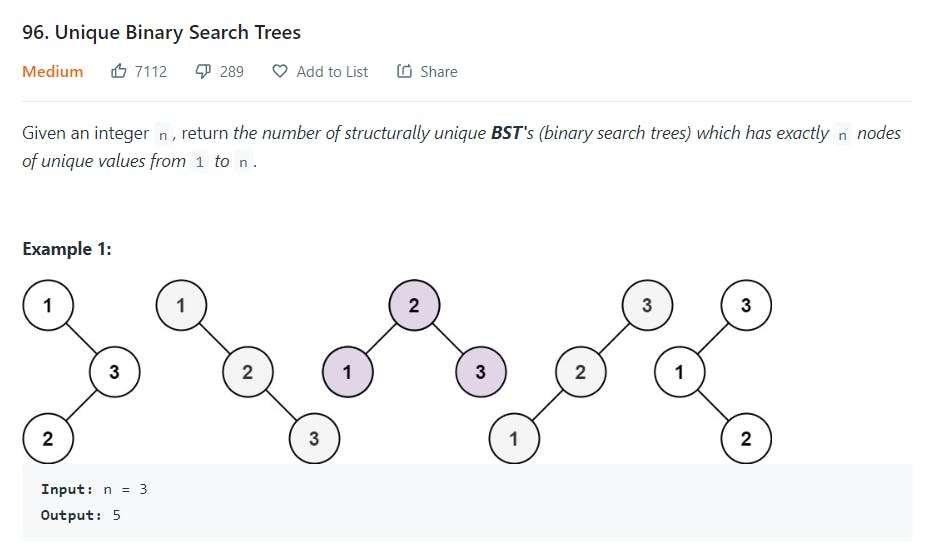
Question Link: leetcode.com/problems/unique-binary-search-..

class Solution {
    public int numTrees(int n) {
        int[] dp = new int[n]; // use dynamic programming for more faster calculation
        Arrays.fill(dp, -1); // initialize all elements inside array as -1.
        return catalanNumber(n, dp);
    }

    public int catalanNumber(int n, int[] dp){
        int res = 0;
        if(n <= 1){
            return 1;
        }
        if(dp[n - 1] != -1){ 
            // if we already perform calculation on n we simply return its value
            return dp[n-1];
        }
        for(int i = 0; i<n; i++){
            // use catalan number formula
            res += catalanNumber(i, dp) * catalanNumber(n-i-1, dp);
        }
        // store the calculated value to the dp array
        return dp[n-1] = res;
    }
}

Practice Question

Q. Number of correct bracket sequences consisting of n opening and n closing brackets.

Q. The number of non-isomorphic full binary trees with 'n' internal nodes (i.e. nodes having at least one son).

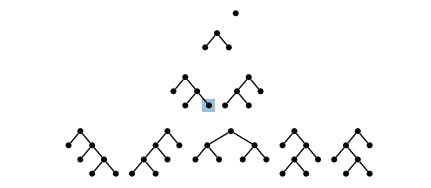
Conclusion

We can use different strategies to apply catalan number algorithm. If we use it with the Dynamic Programming concepts it smooth out and take much less time but we required space for storing the values in DP. There is one more approach which use binomial coefficient which is also faster and doesn't require any extra space.

So we can use it according to our given conditions and requirement.

Subscribe to the newsletter to read more blogs on data structures and algorithms!